简要介绍

本论文已经被 ICASSP 2024 接收，主要解决的问题是声学回声消除中存在延时和非线性失真情况下消除效果不好的问题。解决的方式为：

  1. 采用 dual-path alignment (DPA) 实现网络的隐式对齐，改善存在延时情况下的声学回声消除性能。
  2. 采用两阶段网络来实现更好去除非线性情况下的回声。第一阶段估计幅度谱掩膜，第二阶段估计相位谱来实现回声消除。

image-20240310133101655

问题描述

image-20240310132743405

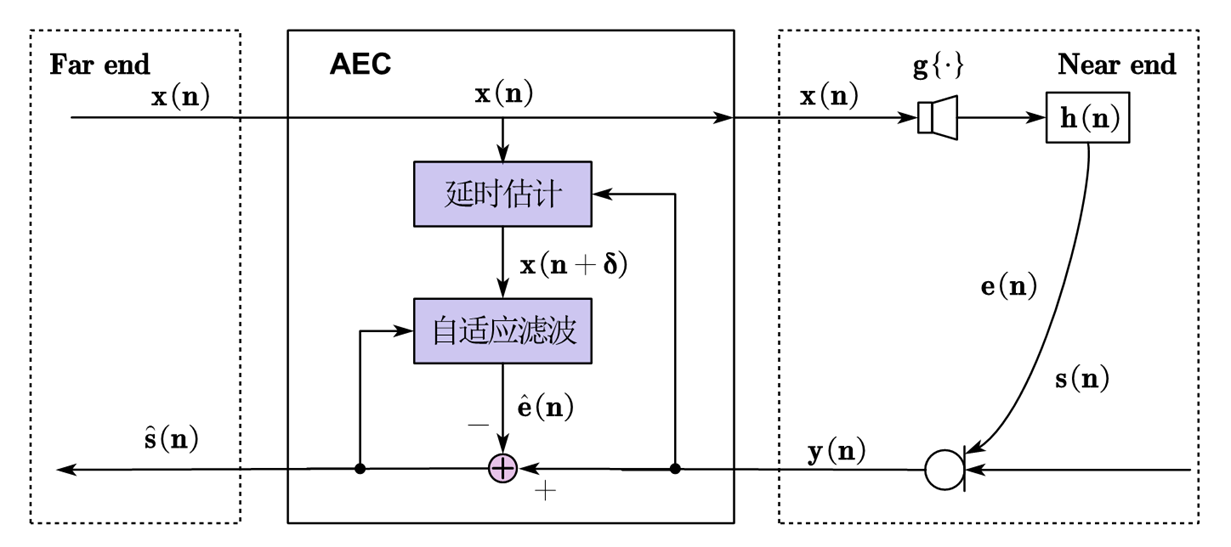
如下图，近端麦克风信号 $y(n)$ 包含回声信号 $e(n)$ 和 语音信号 $s(n)$ :

$$ y(n) = s(n) + e(n) $$

其中声学回声信号由远端参考信号 $x(n)$ 经过扬声器的非线性失真函数 $g(\cdot)$ 并和回声路径进行卷积得到 $h(n)$ .

$$ e(n) = h(n)*g(x(n)) $$

本文会在频域进行回声消除任务，所以会有如下表达式：

$$ Y(t,f) = S(t,f)+ E(t,f) $$

其中 $t,f$ 分别代表帧索引和频点索引，整个回声消除的目的就是从 $Y(t,f)$ 中去除 $E(t,f)$ 并保留 $S(t,f)$ 。

网络结构

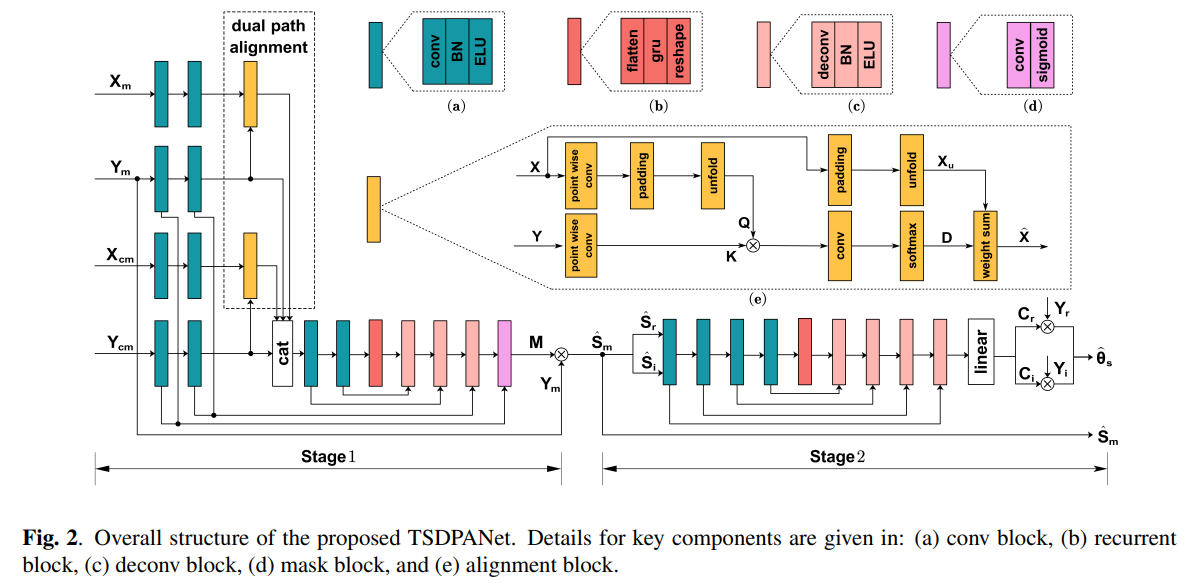
image-20240310134257126

网络整体结构如上，包含两阶段。第一阶段会估计一个幅度谱掩膜用于增强近端麦克风信号（并且DPA用来软对齐信号），第二阶段会估计一个复数谱掩膜用于矫正相位。

第一阶段

第一阶段网络由 CRN 构成：包含 encoder block，recurrent block 和 decoder block。 encoder 会接收四路信号的输入： $X_m(t,f),X_{cm}(t,f),Y_m(t,f), Y_{cm}(t,f)$ 分别代表远端参考信号的幅度和压缩幅度谱，近端麦克风信号的幅度和压缩幅度谱。四路输入首先各自经过两层卷积来提取特征。然后送入 DPA 模块得到对齐后的远端参考信号的特征，并拼接在一起经过额外两层卷积来进一步提取特征。encoder的输出会送到 recurrent block 进一步获取帧之间的信息，最后使用 decoder 来估计幅度谱的掩膜 $M(t,f)$ 。

从而估计出来的幅度谱为：

$$ \hat S_m(t,f) = M(t,f)\odot Y_m(t,f) $$

第二阶段

第二阶段网络同样由 CRN 构成。encoder 的输入包含估计出来的近端信号的实部和虚部，其通过下式计算：

$$ \hat S_{r}(t,f) = \hat S_m(t,f)cos(\theta_y(t,f))\\ \hat S_{i}(t,f) = \hat S_m(t,f)sin(\theta_y(t,f)) $$

其中 $\theta_y(t,f)$ 代表 $Y(t,f)$ 的相位谱。然后网络会估计出一个复数谱掩膜 $[C_r(t,f), C_i(t,f)]$ 。通过该复数谱我们可以估计出近端语音的相位：

$$ \hat \theta_s(t,f) = arctan(\frac{C_i(t,f)Y_i(t,f)}{C_r(t,f)Y_r(t,f)}) $$

最后估计出来的干净语音由下式求得：

$$ \hat S(t,f) = \hat S_m(t,f)e^{j\hat \theta_s(t,f)} $$

损失函数

损失函数包含两部分：压缩幅度谱损失和压缩复数谱损失。

$$ L_{s_1} = \frac{1}{TF}\sum_{t,f}|\hat S_m^{\alpha}(t,f) - S_m^{\alpha}(t,f)|^2\\ L_{s_2} = \frac{1}{TF}\sum_{t,f}|\hat S_m^{\alpha}(t,f)e^{j\hat \theta_s(t,f)} - S_m^{\alpha}(t,f)e^{j\theta_s(t,f)}|^2 $$

然后将这个两个损失函数进行加权得到：

$$ L = \gamma L_{s_1} + (1-\gamma)L_{s_2} $$

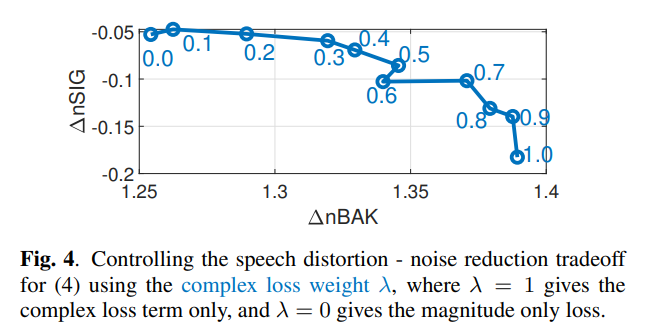
其中 $\gamma$ 的取值通过验证集获得。并且参考自论文 EFFECT OF NOISE SUPPRESSION LOSSES ON SPEECH DISTORTION AND ASR PERFORMANCE，其给出的结论是 幅度谱权重高的时候更加关注语音损伤，复数谱权重高的时候更加关注降噪。

image-20231119133918085

结果

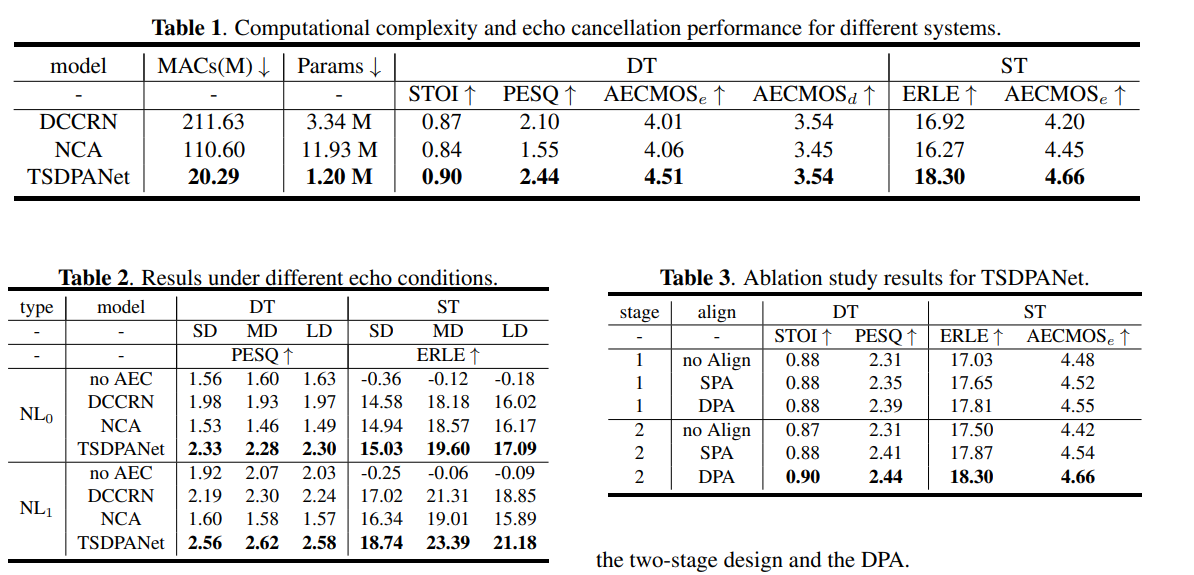
image-20240310142536545

以上是实验结果的汇总。通过 table 1 可以看到提出的 TSDPANet 相比于两个 baseline 在运算量和参数量都较低的情况下能够更加有效提升双讲和单讲下的性能。通过 table 2 可以看出 TSDPANet 在不同延时和存在非线性与否的情况下都能取得良好性能。最后，通过 table 3 中的消融实验可以看出，两阶段网络性能好于一阶段，这是因为两阶段能够更好优化相位。但是在不采用对齐的时候，两阶段网络效果不如一阶段，这主要因为没有对齐影响了第一阶段的幅度谱掩膜估计从而影响了相位估计。此外，通过 SPA 和 DPA 的对比可以看出，采用 DPA 可以取得更好的性能，这可以归功于 DPA 更好的特征提取能力和对齐能力，从而提升了幅度谱的估计和相位的矫正。

另外需要说明的是从 $AECMOS_d$ 的结果看来效果并不是很好，网络不可避免对语音造成了损伤。因为第一阶段的掩膜的损伤无法通过第二阶段来进行补偿。后续考虑对这一部分进行改进，考虑使用DCT变换来将两阶段统一为一阶段。

音频对比

以下是传统算法在高延时 (506ms)，存在非线性失真，双讲情况的效果对比：

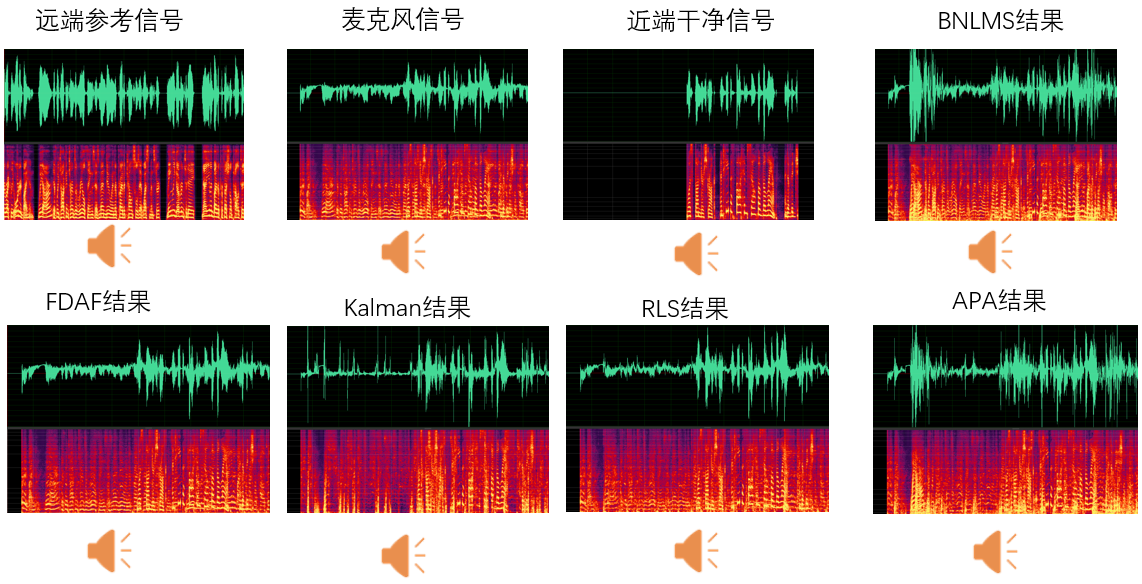
image-20240310170829975

从上图可以看到，效果非常差，这是因为在有延时情况下传统算法将无法正确估计回声路径，这导致了无法正确抑制回声。此外双讲和非线性也严重影响了各类算法的收敛，导致效果不好。

以下是论文中 baseline 与提出的网络的对比：

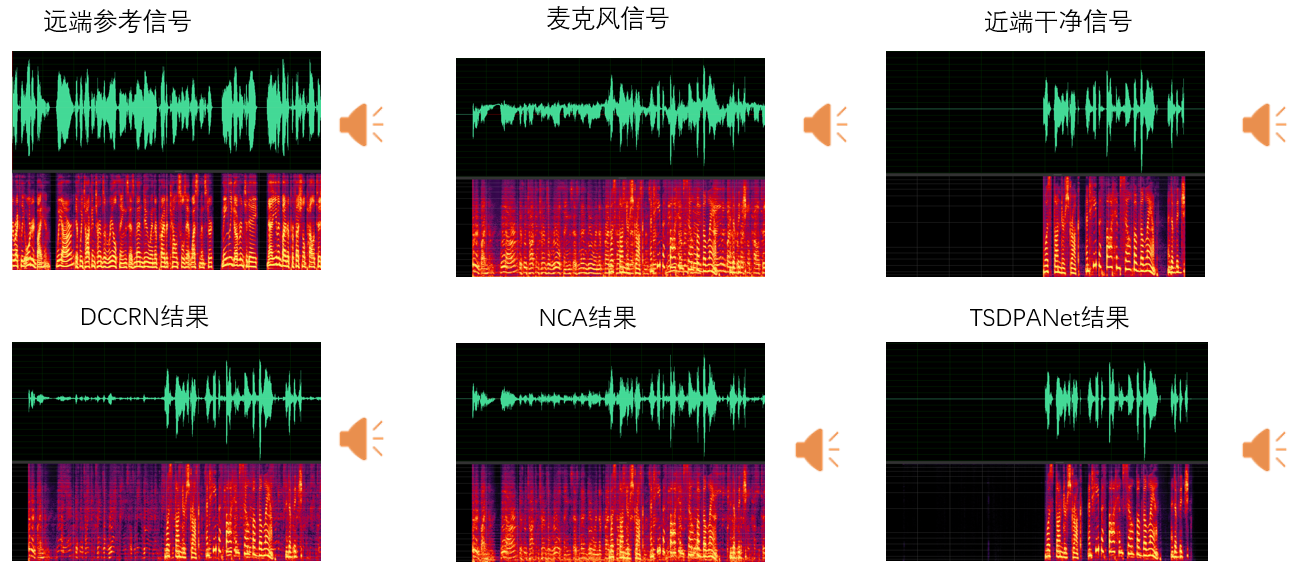
image-20240310171003427

可以看到其他 baseline 的效果并不好，一方面是因为没有进行对齐，另一方面在于提出的两阶段网络能够更好地处理复杂情况下的回声。

但从 TSDPANet 和近端干净信号的对比可以看出，TSDPANet还是存在一定的语音损伤的。

More about alignment

如何通过网络实现软对齐的：核心在于将原来的帧内自相关，改为了求取帧间自相关。

首先由于需要进行延时的是远端参考信号，所以会在远端参考信号 $X$ 前面进行padding，而近端麦克风信号 $Y$ 则不做处理。

如果延时最长是 $n$ 帧 ，那么按照以下方式进行 $padding$ ：

$$ [padding,\cdots, padding, X(1,f),X(2,f),\cdots,X(k,f)]^T $$

同时 $unfold$ ：

$$ \begin{align} Delay=0&:X_{D_0} = [X(1,f),X(2,f),…,X(k-1,f),X(k,f)]^T\\ Delay=1&:X_{D_1} = [padding,X(1,f),…,X(k-2,f),X(k-1,f)]^T\\ Delay=2&:X_{D_2} = [padding,padding,…,X(k-3,f),X(k-2,f)]^T\\ …\\ Delay=n&:X_{D_n} = [padding,padding,…,X(k-(n-1),f),X(k-n,f)]^T\\ \end{align} $$

所以有：

$$ \begin{align} Q &= [X_{D_n},X_{D_{n-1}},…,X_{D_1},X_{D_0}]^T\\ K &= [Y(1,f),Y(2,f),…,Y(k-1,f),Y(k,f)]\\ \end{align} $$

得到：

$$ \begin{align} D &= softmax{QK^T}\\ &= softmax{ \begin{bmatrix} padding & padding & \cdots & X(k-(n-1),f) & X(k-n,f) \\ \vdots & \ddots & \vdots \\ padding & padding & \cdots & X(k-3,f) & X(k-2, f) \\ padding & X(1,f) & \cdots & X(k-2,f) & X(k-1, f) \\ X(1,f) & X(2,f) & \cdots & X(k-1,f) & X(k, f) \\ \end{bmatrix} \begin{bmatrix} Y(1,f) \\ Y(2,f) \\ \vdots \\ Y(k-1,f) \\ Y(k,f) \\ \end{bmatrix} } \end{align} $$

最后得到 D 为延时概率：

$$ D = [prob_{D_n}, prob_{D_{n-1}},\cdots,prob_{D_0}]^T $$

通过这个概率对 Q ，也就是各个延时的特征进行加权则可以得到最后经过延时的特征：

$$ \hat X = sum[Q\odot D] = QD^T = \sum_{i = 0}^{n}prob_{D_i}X_{D_i} $$

传统做法

To be done！

image-20240310171341685