风噪特性
知己知彼,百战不殆。清楚了解风噪的特性才能够对症下药。
- 高度非平稳性:因为风冲击传感器的产生的信号是快速变化且不稳定的
- 能量集中于中低频:通过频谱特征可以观察到
- 不同麦克风信号的风噪高度不相关:因为传感器之间的湍流是完全不相关的
- 风噪和语音是不相关的
问题描述
假设第一个麦克风接收到的信号为 $y_1(n)$ ,那么其包含语音 $x(n)$ 和风噪信号 $w_1(n)$ :
$$ y_1(n) = x(n) + w_1(n) $$
第二个麦克风接收到的信号为 $y_2(n)$ ,那么其包含语音 $x(n)$ 和风噪信号 $w_2(n)$ :
$$ y_2(n) = x(n) + w_1(n) $$
其中默认对麦克风信号进行了对齐以保证 $x(n)$ 在麦克风信号里是一致的。
然后将两路麦克风信号通过短时傅里叶变换得到:
$$ Y_1(t,f) = X(t,f) + W_1(t,f)\\ Y_2(t,f) = X(t,f) + W_2(t,f) $$
风噪抑制的目标就是从两路麦克风信号 $Y_1(t,f),Y_2(t,f)$ 中恢复出 $X(t,f)$ 。
方法
整体方法如下图所示:
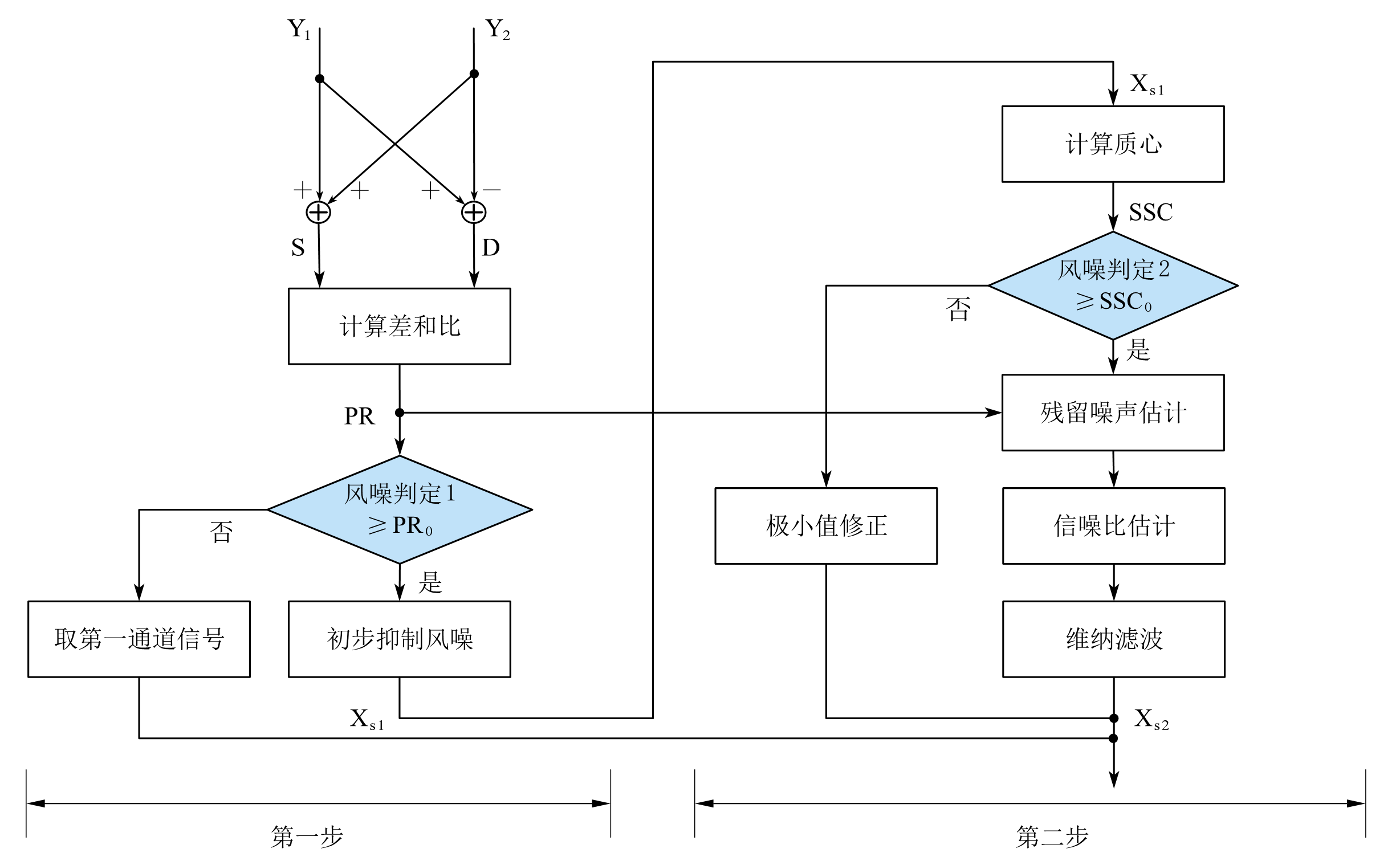
分为两阶段对风噪进行消除:第一阶段通过差和比来判断是否存在风噪,如果存在风噪则采用双麦的空间相关性和相似性的公式进行初步风噪抑制,不存在则直接输出。如果第一阶段存在风噪,那么第二阶段会再次采用质心法判断是纯风噪信号还是带残留风噪的信号,如果是残留风噪信号则进行残留风噪估计并进行维纳滤波。如果是纯风噪信号则使用一个极小值对其进行修正。
以下是细节介绍:
第一阶段
通过两路麦克风信号可以得到差信号 $D(t,f)$ 和和信号 $S(t,f)$ 如下:
$$ \begin{align} D(t,f) &= Y_1(t,f) - Y_2(t,f) = W_1(t,f) - W_2(t,f)\\ S(t,f) &= Y_1(t,f) + Y_2(t,f) = 2X(t,f)+W_1(t,f)+W_2(t,f) \end{align} $$
计算对应的功率谱:
$$ \begin{align} \Phi_{D}(t,f) &= E[|D(t,f)|^2] = \Phi_{W_1}(t,f) + \Phi_{W_2}(t,f)\\ \Phi_{S}(t,f) &= E[|S(t,f)|^2] = 4\Phi_X(t,f) + \Phi_{W_1}(t,f) + \Phi_{W_2}(t,f) \end{align} $$
对其进行平滑操作:
$$ \Phi_D(t,f) = \alpha_d \Phi_D(t-1,f) + (1-\alpha_d)|D(t,f)|^2\\ \Phi_S(t,f) = \alpha_s \Phi_S(t-1,f) + (1-\alpha_s)|S(t,f)|^2 $$
由此可以求得差和比 $PR(t,f)$:
$$ PR(t,f) = \frac{\Phi_D(t,f)}{\Phi_S(t,f)} = \frac{\Phi_{W_1}(t,f) + \Phi_{W_2}(t,f)}{4\Phi_X(t,f) + \Phi_{W_1}(t,f) + \Phi_{W_2}(t,f)} $$
当风噪占主导时候差和比为1,当语音占主导的时候差和比为0:
$$ \begin{align} lim_{\Phi_{D}\rightarrow \infty}PR(t,f) = 1\\ lim_{\Phi_{S}\rightarrow \infty}PR(t,f) = 0\\ \end{align} $$
为了结合风噪特性,在计算差和比的时候只取中低频进行计算,并求取平均:
$$ \overline{PR}(t) = \frac{1}{k_2-k_1+1}\sum_{k=k_1}^{k_2}w(k)PR(t,k) $$
那么就可以通过 设置差和比阈值 $PR_0$ 来判断当前帧为语音还是带风噪:
$$ IsWind(t) = \begin{cases} \ 1, & \overline{PR(t)}\ge PR_0\\ \ 0, & \overline{PR(t)} < PR_0 \end{cases} $$
如果是风噪则通过下式进行抑制,该公式考虑了双麦的空间相关性和相似性:
$$ X_{s1}(t,f) = Y_1(t,f) + \frac{1+j\lambda}{1+\lambda^2}(Y_2(t,f)-Y_1(t,f)) $$
其中 $\lambda = \frac{|Y_2(t,f)|}{Y_1(t,f)}$ 。
如果不是风噪则直接输出,不做处理。
第二阶段
对于经过第一阶段风噪抑制的信号可能还会存在风噪残留,所以需要进行进一步的处理。
因此在第二阶段会采用质心法求解第一阶段得到的信号的质心,进行风噪的检测 :
$$ SSC(t) = \frac{sr}{N}\frac{\sum_{k=1}^{k_3}k\Phi_{s1}(t,f)}{\sum_{k=1}^{k_3}\Phi_{s1}(t,f)} $$
其中 $sr$ 为信号采样率, $N$ 为信号的进行傅里叶变换的点数,$\Phi_{s1}(t,f)$ 是第一阶段输出的信号的平滑功率谱,通过下式计算:
$$ \Phi_{s1}(t,f) = \alpha_{s1}\Phi_{s1}(t-1,f) + (1-\alpha_{s1}) |X_{s1}(t,f)|^2 $$
那么就可以通过设置质心的阈值 $SSC_0$ 来判断当前帧是纯风噪还是带风噪信号 :
$$ IsNoisySpeech(t) = \begin{cases} \ 1, & \overline{SSC(t)}\ge SSC_0\\ \ 0, & \overline{SSC(t)} < SSC_0 \end{cases} $$
如果是纯风噪则直接进行最小值修正 :
$$ X_{s2}(t,f) = \gamma X_{s1}(t,f) $$
如果是带噪语音则进行维纳滤波 ,首先通过下式求解残留风噪的功率:
$$ \Phi_{W}(t,f) = PR(t,f) X_{s1}(t,f) $$
然后求得先验信噪比:
$$ \xi(t,f) = \alpha_{\xi}\xi(t-1,f) + (1-\alpha_{\xi})MAX[\frac{X_{s1}(t,f)-\Phi_W(t,f)}{\Phi_W(t,f)},0] $$
从而求得频率域维纳滤波的滤波器为:
$$ H(t,f) = \frac{\xi(t,f)}{\xi(t,f)+1} $$
得到二阶段输出为:
$$ X_{s2}(t,f) =H(t,f)X_{s1}(t,f) $$
参数选择
超参数一共有如下:
- $\alpha_d$ :差信号功率谱的平滑系数,选择0.7
- $\alpha_s$ :和信号功率谱的平滑系数,选择0.7
- $\alpha_{s1}$ :第一阶段输出信号功率谱的平滑系数,选择0.8
- $\alpha_{\xi}$ :先验信噪比的平滑系数,选择0.5
- $PR_0$ :差和比阈值,取值0.15
- $SSC_0$ :质心阈值,取值175
- $k_1$ :差和比求和下限,取值1,关注0Hz以上的信号差和比
- $k_2$ :差和比求和上限,取值91,关注3000Hz以下的信号差和比 (3000·/8000*241+1)
- $k_3$ :质心法求和上限,取值31,关注1000Hz以下的质心(1000/8000*241+1)
- $\gamma$ :用于修正的最小值,取值0.001,用于完全抑制纯风噪信号
- $N$ :傅里叶点数, 取值480
- $sr$ :采样率,取值16000
下面针对差和比阈值和质心的阈值进行介绍。
差和比阈值
以下是干净语音,纯风噪,带噪语音的差和比对比。可以看到风噪的差和比基本都大于0.2,而带风噪则基本大于0.15,而语音的差和比则非常小。因此选取0.15作为阈值判断。
此外一个显然的特性是,随着风速的增强(风噪的增强),带风噪的信号差和比逐渐趋近于1,符合前述分析。
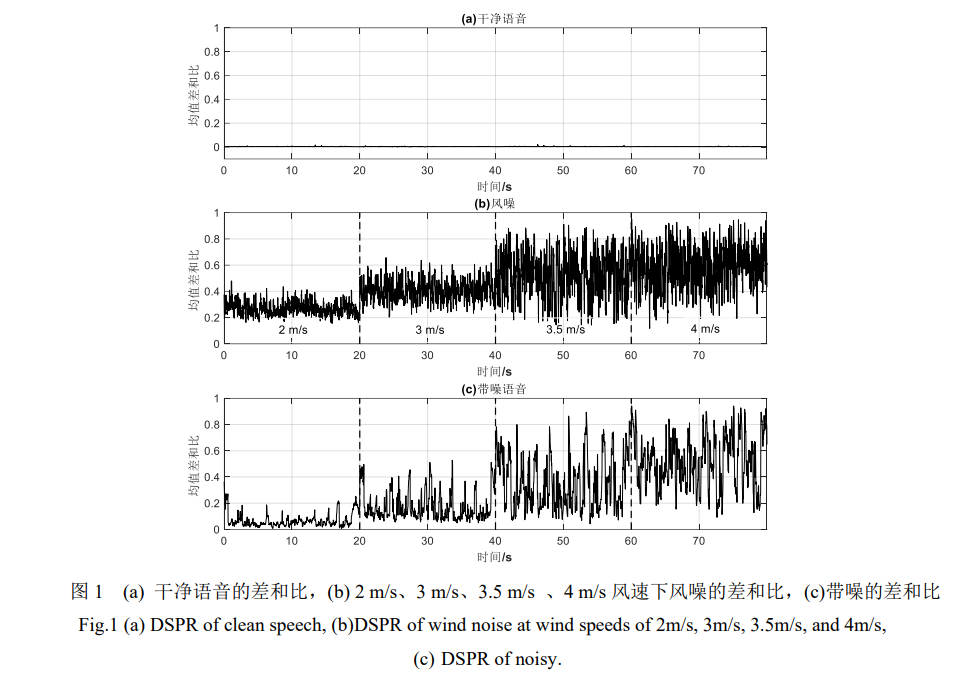
如果选取阈值小于0.15,会使得将更多语音认为是带噪语音,如果将阈值设置更大,则会漏检一部分的风噪。所以在设置的时候要特别关注。
质心阈值
在 2-3m/s 风速下,风噪的质心会比带噪语音质心小。随着风速的增加,风噪质心增大,当风速大于 3.5m/s 时,风噪质心基本与带噪语音信号相当。故可以通过质心判别信号是风噪还是带噪语音信号。着重优化高风速下的算法性能。这里选取175,则是参考高风速下的质心分布。
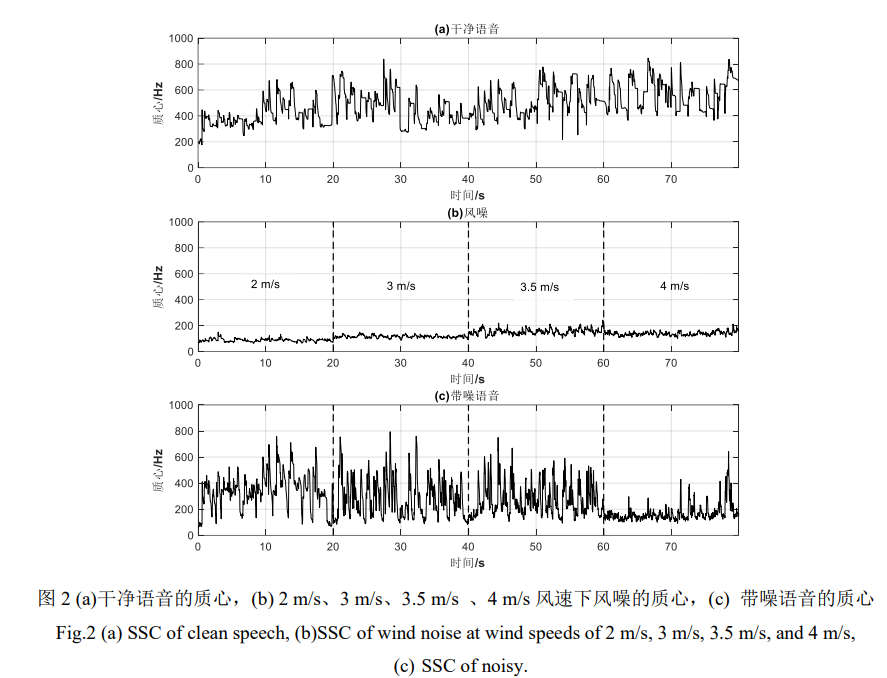
如果提升SSC阈值,会使得纯风噪无法被检测,如果降低这个阈值将会有更多风噪信号被认为带噪信号。
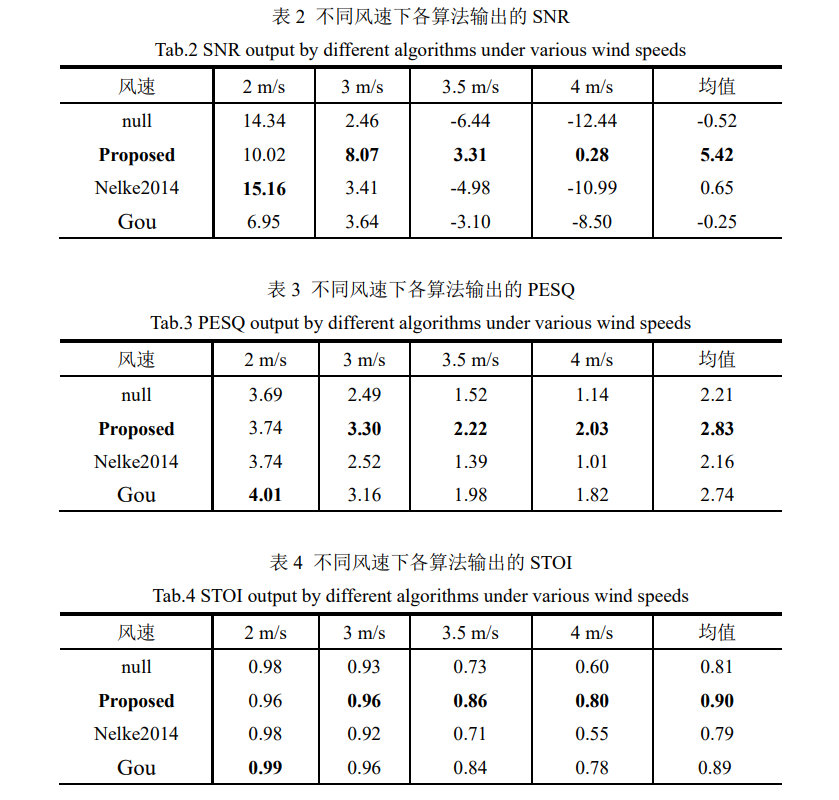
效果
可以看到一阶段针对风速较低的风噪去除较好,但仍旧有残留,且高风噪段消除效果不明显。经过第二阶段之后则将风噪很好地进行了去除。
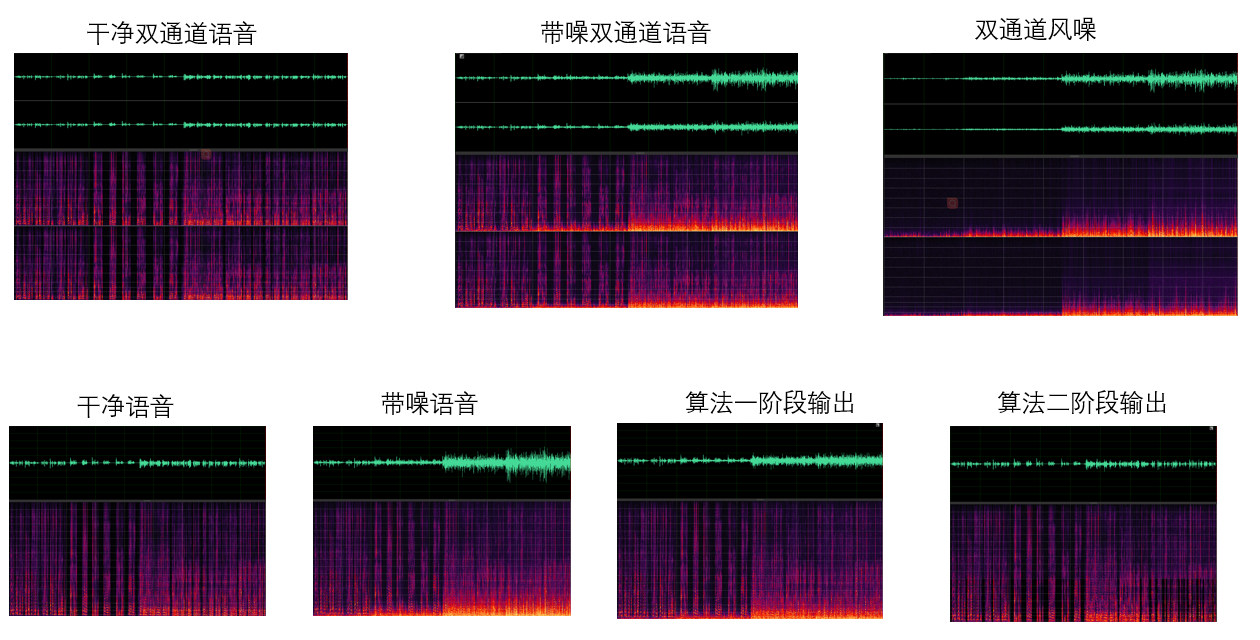
从下表也可以看出,提出的方法在风速越高的情况下效果远优于其他算法。缺点也很明显,在低风速情况下效果还有待提升。